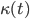Multivariable Calculus Mathematica commands
Here are the commands I find most useful for MA 242: Multivariable Calculus.
General Algebra and Calculus |
Jump to next Unit |
|---|
The following items are useful throughout the course.
Using mathematical functions
Existing functions in Mathematica are capitalized and use square brackets. Example:
Cos[x]
Sin[Pi/3]
Log[7] % this is natural log
Exp[.4*x] % this is e^(.4x)
Simplifying Answers
Try appending //Simplify or //FullSimplify at the end of any answer. Example:
Cos[x]^2 + Sin[x]^2 // FullSimplify
Avoiding hyperbolic trig functions
Try appending //TrigToExp after an answer. Example:
ArcTanh[u^2] // TrigToExp
Returning answers as a decimal:
Append //N at the end of any answer. Example:
Sqrt[3]/17 // N
Solving Equations
Solve an equation in Mathematica.
Solve[x^2==9,x]
Solve[x^2-2*x-6==0,x]
Getting answers with the imaginary number 
Mathematica allows for complex numbers. Remove them by insisting the variables are real:
Solve[2212 == 1467*Exp[13*t], t!Element] should get converted to the "is an element of" symbol
.
Example: find the general form
for the plane
Solve[{3,2,6}.({x,y,z}-{-1,3,2})==0,z]This will return the plane in the form
Rearrange terms to get the general form.
You can also solve a system of equations, e.g.
Solve[3*x+4*y==7 && 2*x-y==-3,{x, y}]
Single Variable Calculus
This is how you define a function of one variable (used for curves in Unit 2):
f[x_]:=x^2+Sin[x]
How to differentiate:
f'[x]
or
D[f[x],x]
(The latter is more similar to partial derivatives in Unit 3.)
To compute the derivative at a certain value, like 
use "slash-dot:"
f'[x]/.x->4
How to compute the indefinite integral 
(does not include 
):
Integrate[f[x],x]
Definite integral 
Integrate[f[x],{x,0,5}]
Unit 1. Vector Computations |
Jump to next Unit |
|---|
We will use need dot products, cross products, and vector magnitudes in many computations throughout the course (especially in Unit 6 and Unit 7), so I hope these commands in particular assist you.
Dot Product
Calculate the dot product (inner product) of two vectors.
Dot[{a1,b1,c1},{a2,b2,c2}]
u.v
Example:
Dot[{2,3,1},{1,-1,4}] % Computes the dot product of {2, 3, 1} and {1, -1, 4}
{2,3,1}.{1,-1,4} % Computes the dot product of {2, 3, 1} and {1, -1, 4}
Cross Product
Save yourself several minutes and compute the cross product of two vectors--I recommend doing this in parallel to your written work so that you can check yourself as you move through problems.
Cross[{a1,b1,c1},{a2,b2,c2}]
Example:
Cross[{2,3,1},{1,-1,4}] % Computes the cross product of {2, 3, 1} and {1, -1, 4}
Vector Magnitude
Since 
we can calculate the magnitude (length) of a vector using Sqrt and Dot.
Sqrt[v.v]
Example:
u={3,4,5}
Sqrt[u.u] % Computes the magnitude of vector {3, 4, 5} using the dot product
Angle between vectors
This is a combination of dot and magnitude, with ArcCos. The answer will be in radians:
ArcCos[u.v/Sqrt[u.u*v.v]]
To get the angle in degrees, just convert this from radians to degrees...
ArcCos[u.v/Sqrt[u.u*v.v]]*180/Pi
Projection of 
onto 
There is a command for this, but why bother when it can be done using the definition of projection? 
(u.v)/(v.v)*v
Example:
u={3,4,5};
v={1,1,1}
(u.v)/(v.v)*v % Computes the projection of {3, 4, 5} onto {1, 1, 1}
Unit 2. Parametric Curves |
Jump to next Unit |
|---|
Be sure to see the page Curve Quantities. In many of these computations, it may be useful to append //FullSimplify onto the end of your command.
Define a curve 
in parametric form:
r[t_]:={x[t],y[t],z[t]}
Example:
r[t_]:={2*Cos[t],2*Sin[t],t}
Plotting a curve in 3D-space:
ParametricPlot3D[r[t],{t,0,6*Pi}]
Computing velocity, speed, and acceleration:
r'[t] Sqrt[r'[t].r'[t]] r''[t]
This is just a combination of earlier commands based on the literal definition of 
T[t_]:=r'[t]/Sqrt[r'[t].r'[t]]
Arc Length
Given that 
this computation is another combination of earlier commands on this page. Here is an example computing the length of a parametric curve from 
to 
Integrate[Sqrt[r'[t].r'[t]],{t,0,6}]
Figuring out how to use prior commands (like to create 
) to compute the curvature is Exercise 5 in Mathematica Lesson 6 - Curves 2.
Again, a combination of prior commands based on the definition 
T'[t]/Sqrt[T'[t].T'[t]]
Again, a combination of prior commands based on the definition 
Cross[T[t],N[t]]
Unit 3. Differentiable Multivariable Calculus |
Jump to next Unit |
|---|
Creating a Function of Multiple Variables
To define a function of multiple variables in Mathematica, use the following syntax:
f[x_,y_]:=x^2+y^2
g[x_,y_,z_]:=Sin[x]+Cos[y]-Exp[z]
Graphing 
Plot3D is used to plot a function of two variables in a 3D space. In the example below, a previously defined function 
is being plotted on the domain 
Plot3D[f[x y],{x,-2,2},{y,-3,3}]
Creating contour diagrams
ContourPlot can be used to visualize level curves for a function of two variables. In the example below, the level curves for a previously defined function are
being plotted on the domain
ContourPlot[f[x,y],{x,-2,2},{y,-3,3}]
Plotting parametric surfaces
ParametricPlot3D can be used to plot a parametric surface. Below is how to plot the surface parametrized as 
ParametricPlot3D[{Sin[u],Cos[v],u+v},{u,0,2*Pi},{v,0,2*Pi}]
Partial Derivatives
Partial derivatives of a function of multiple variables can be computed using the following syntax:
D[f[x,y],x] % Partial derivative with respect to x
D[f[x,y],y] % Partial derivative with respect to y
Example: To find the partial derivatives of the function 
, use the following commands:
D[f[x,y],x]
D[f[x,y],y]
Example:
D[x^2+y^3,x] % Outputs 2x
D[x^2+y^3,y] % Outputs 3y^2
To compute the derivative at a certain value, like 
use "slash-dot:"
D[f[x,y],x]/.x->4/.y->-1
Gradient
Compute the gradient of a function.
Grad[f[x,y],{x,y}]
Example:
Grad[x^2+y^3,{x,y}] % Outputs {2x, 3y^2}
Evaluated at 
Grad[x^2+y^3,{x,y}]/.x->-3/.y->7
Directional Derivatives
For differentiable functions, 
where 
is a unit vector. Below is an example of computing this for a pre-existing function and a vector which is not unit length:
a=10
b=5
v={3,2}
u=v/Sqrt[v.v]
Grad[f[x,y],{x,y}].u/.x->a/.y->b
Linearization of 
at a point 
Recall 
is the linearization of 
at 
It is best to set up the right-hand side in two steps:
a=4
b=-1
Df=Grad[f[x,y],{x,y}]/.x->a/.y->b
L[x_,y_]:=f[a,b]+Dot[Df,{x-a,y-b}]
Critical points for 
We want to find when 
so combine earlier techniques:
Solve[Grad[f[x,y],{x,y}]=={0,0},{x,y}]
Unit 4 and Unit 5: Multiple Integrals |
Jump to next Unit |
|---|
The following sections detail how to approach multiple integrals using Mathematica, including the usage of different coordinate systems such as rectangular, polar, and spherical coordinates.
Integration in Rectangular Coordinates
Following Fubini's Theorem, double and triple integrals in Mathematica can be set up as iterated integrals. For example, here are the integrals 
and 
Integrate[Integrate[x^2 + y^2, {y, 0, x}], {x, 0, 1}]
Integrate[Integrate[Integrate[x^2 + y^2 + z^2, {z, 0, 1}], {y, 0, x}], {x, 0, 1}]
Integration in Polar Coordinates
The idea is the same, we just convert any integrands to polar coodinates and include the factor of 
In the examples below, I use t for 
Integrate[Integrate[r^2, {r, 0, 1}], {t, 0, 2*Pi}]
Integrate[Integrate[(r*Cos[t]+r*Sin[t])*r,{r,0,2}],{t,0,2*Pi}]
Integration in Spherical Coordinates
Again, same idea, just with different coordinates. I recommend using R for 
p for 
and t for 
Examples of triple integrals in spherical coordinates in Mathematica:
Integrate[Integrate[Integrate[R^2 Sin[p], {R, 0, 1}], {p, 0, Pi}], {t, 0, 2*Pi}]
Visualizing Domains in Rectangular Coordinates
We can use the RegionPlot function to visualize regions in the xy-plane and RegionPlot3D for regions in 
Examples:
RegionPlot[x^2 + y^2 <= 1, {x, -1, 1}, {y, -1, 1}]
RegionPlot3D[x^2 + y^2 + z^2 <= 1, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}]
Unit 6. Line and Surface Integrals |
Jump to next Unit |
|---|
The following items will guide you through line and surface integrals, vector fields, and related computations in Mathematica.
Creating Vector Fields
Define vector fields using a function definition, but ideally with "vector inputs" (use curly brackets). Examples:
F[{x_,y_}] := {x^2, 1-y}
F[{x_,y_,z_}] := {x, y+z, Exp[x+z]}
Visualizing Vector Fields
VectorPlot[F[{x, y}], {x, -3, 3}, {y, -3, 3}]
StreamPlot[F[{x, y}], {x, -3, 3}, {y, -3, 3}]
Computing the Curl and Checking for a Conservative Field
In this unit, we compute the curl of a 2D vector field to check if it is conservative:
Curl[F[{x, y}], {x, y}] // FullSimplify
(We revisit this notion in Unit 7.)
Computing Scalar Line Integrals
Set up and compute scalar line integrals using a parameterized curve and a scalar function. Follow the four-step process from lecture. Example:
f[{x_,y_,z_}] := 2-z
r[t_] := {Cos[t], 0, Sin[t]}
magr = Sqrt[r'[t].r'[t]] // FullSimplify
Integrate[f[r[t]]*magr, {t, 0, Pi}]
Computing Vector Line Integrals
Follow the process outlined in lecture. Example setup:
F[{x_,y_}] := {2-y,x^2+y^2}
r[t_] := {Cos[t], Sin[t]}
Integrate[F[r[t]].r'[t], {t, 0, 2*Pi}]
Creating Parametric Surfaces
Create parametric surfaces using function definitions. Example:
r[u_,v_] := {u*Cos[v], u*Sin[v], u^2}
Computing Scalar Surface Integrals
We need to parametrize the surface, compute the magnitude of the cross product of the partial derivatives, and integrating the 
over the surface. Step-by-step guide based on Example 1 from Unit 6 Lecture 13: Scalar surface integrals (15:56):
1-2. Define the function and the parametric surface 
r[u_, v_]={u*Cos[v],u*Sin[v],9-u^2}
f[{x_,y_,z_}]:=x*y
3. Compute the partial derivatives 
and 
and the the magnitude of the cross product 
Notice this code is re-usable for any such setup (it's all done with general variables and not specific terms):
ru=D[r[u,v],u]
rv=D[r[u,v],v]
n=Cross[ru,rv]//FullSimplify
magN=Sqrt[n.n]
4. Integrate over the bounds on 
and 
Integrate[Integrate[f[r[u,v]]*n,{u,0,Pi/2}],{v,0,2}]
Computing Vector Surface Integrals
We need to parametrize the surface, compute the magnitude of the cross product of the partial derivatives, and integrating the over the surface. Step-by-step guide based on Example 1 from Unit 6 Lecture 14: Flux Integrals (22:06):
1-2. Define the vector field 
and the parametric surface
r[u_, v_]={Cos[v],Sin[v],-u/Sqrt[1-u^2]}
F[{x_,y_,z_}]:={-y,-x,1}
3. Compute the partial derivatives and and the the magnitude of the cross product Notice this code is re-usable for any such setup (it's all done with general variables and not specific terms):
ru=D[r[u,v],u]
rv=D[r[u,v],v]
n=Cross[ru,rv]//FullSimplify
(you may need to assess on your own if the above vector n is pointing in the correct direction).
4. Integrate over the bounds on and
Integrate[Integrate[F[r[u,v]].n,{u,0,1}],{v,0,2*Pi}]
Unit 7. Vector Analysis |
Jump to top |
|---|